Ngram Prompt Lookup Decoding

In cases where you don't have a draft model available, you can use ngram prompt lookup decoding to perform speculative decoding with LLMs.

This method involves gathering the candidate sequences from the input text itself. If the latest generated ngram is in the input, use the continuation as a candidate.

You can use this method like this:

from aphrodite import LLM, SamplingParams

prompts = [
    "The future of AI is",
]
sampling_params = SamplingParams(temperature=0.8, top_p=0.95)

llm = LLM(
    model="facebook/opt-6.7b",
    tensor_parallel_size=1,
    speculative_model="[ngram]",  
    num_speculative_tokens=5,  
    ngram_prompt_lookup_max=4,  
    use_v2_block_manager=True,  
)
outputs = llm.generate(prompts, sampling_params)

for output in outputs:
    prompt = output.prompt
    generated_text = output.outputs[0].text
    print(f"Prompt: {prompt!r}, Generated text: {generated_text!r}")

Or with the CLI:

aphrodite run facebook/opt-6.7b --speculative-model '[ngram]' --num-speculative-tokens 5 --ngram-prompt-lookup-max 4 --use-v2-block-manager

Technical Details

Reference:

• GitHub
• Blog: Break the Sequential Dependency of LLM Inference Using Lookahead Decoding

This method is implemented using the Jacobi method. We break the sequential dependency in autoregressive decoding by concurrently extracting and verifying n-grams directly with the LLM. This method functions without the need for a draft model or a data sore. It linearly decreases the number of decoding steps directly correlating with the log(FLOPs) used per decoding step.

The key observation enabling lookahead decoding is that, although decoding multiple next tokens in one step is infeasible, an LLM can indeed generate multiple disjoint n-grams in parallel. These n-grams could potentially fit into future parts of the generated sequence. This is achieved by viewing autoregressive decoding as solving nonlinear equations and adapting the classic Jacobi iteration method for parallel decoding. The generated n-grams are captured and later verified, if suitable, integrated into the sequence.

Lookahead decoding is able to generate n-grams each step, as opposed to producing just one token, hence reducing the total number of decoding steps -- generating N tokens in less than N steps. In fact, lookahead decoding stands out because it:

• Operates without a draft model, streamlining deployment.
• Linearly reduces the number of decoding steps relative to log(FLOPs) per step.

Background

The Jacobi iteration method is a classic solver for non-linear systems. In the case of LLM inference, we can also employ it for parallel token generation without a draft model. To see this, let's reconsider the autoregressive decoding process. Traditionally, this process is seen as a sequential generation of tokens, illustrated in Figure 2(Left). With some simple rearrangements of equations, it can be conceptualized as solving a system of non-linear equations, as depicted below.

Autoregressive decoding as a process of solving non-linear systems.

An alternative approach based on Jacobi iteration can solve all of this nonlinear system in parallel as follows:

• Start with an initial guess for all variables $y=[y_1,y_2,...,y_m]$
• Calculate new $y^{\prime }$ values for each equation with the previous $y$
• Update $y$ with the new $y^{\prime }$ values
• Repeat this process until a certain stopping condition is achieved (e.g., $y=y^{\prime }$)

This process is illustrated below for easier understanding. Jacobi decoding can guarantee solving all variables in at most steps (i.e., the same number of steps as autoregressive decoding) because each step guarantees at least the very first token is correctly decoded. Sometimes, multiple tokens might converge in a single iteration, potentially reducing the overall number of decoding steps. For example, as shown below, Jacobi decoding predicts and accepts two tokens, "computer" and "scientist," in a single step.

Compared to autoregressive decoding, each Jacobi decoding step is slightly more expensive in terms of FLOPs needed because it requires LLM forward computation on >1 token. Fortunately, this usually does not translate into slowdowns, thanks to the parallel processing nature of GPUs.

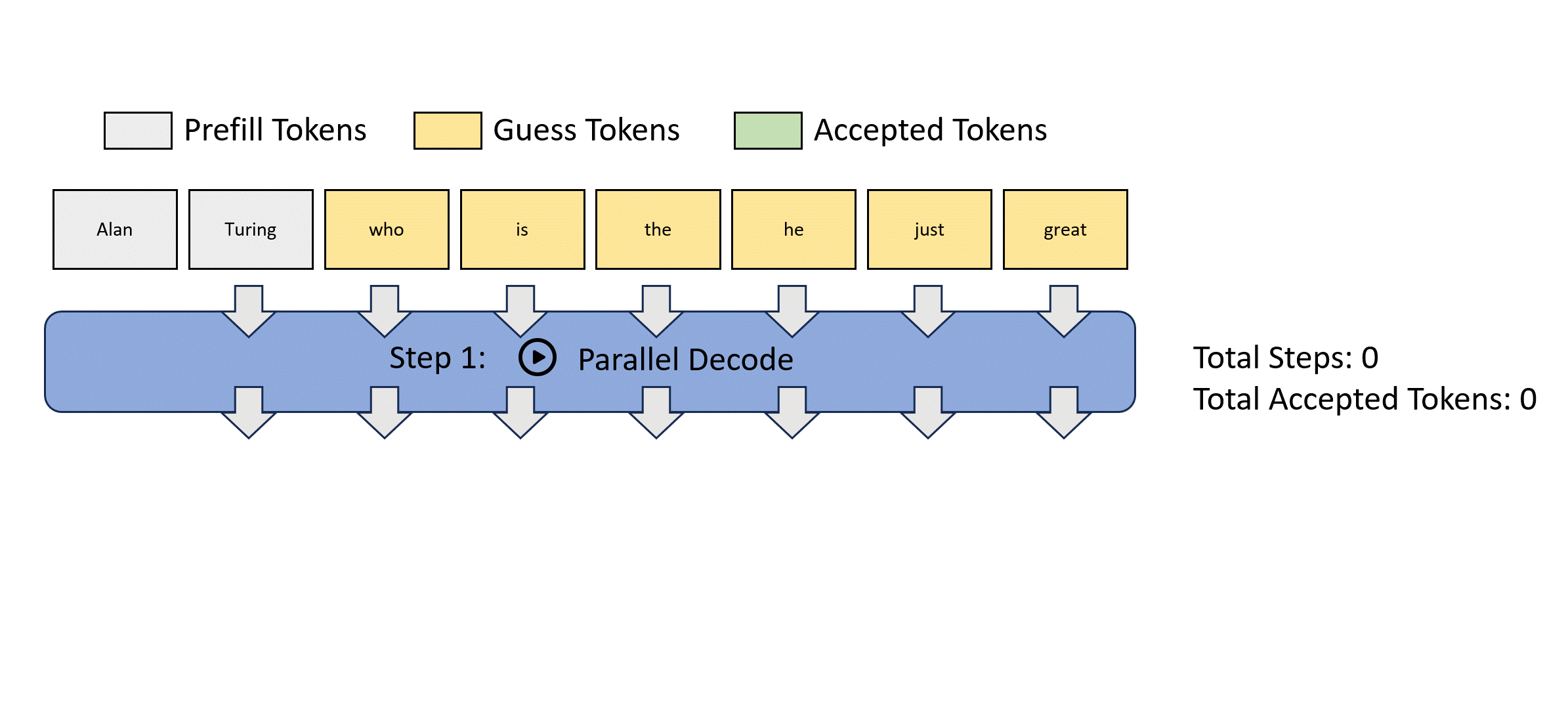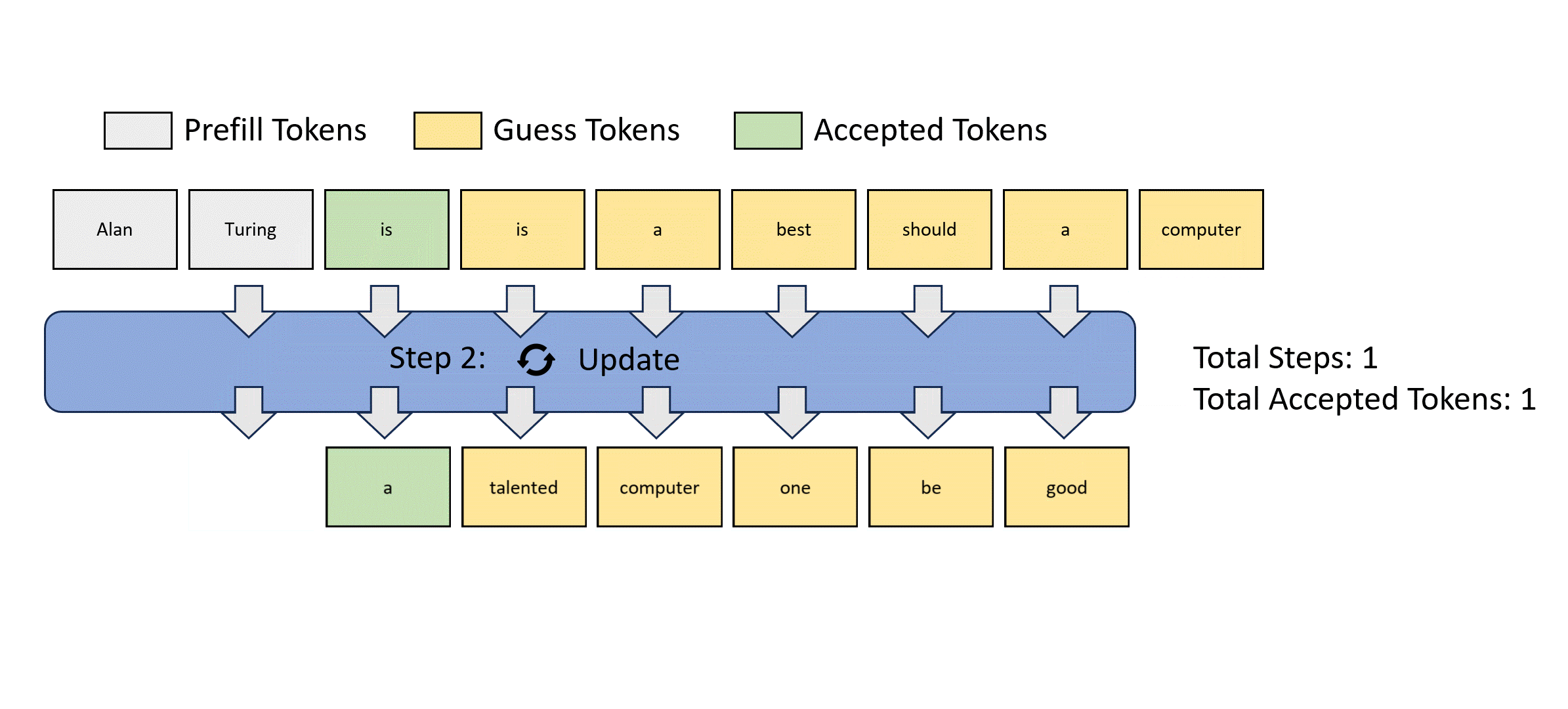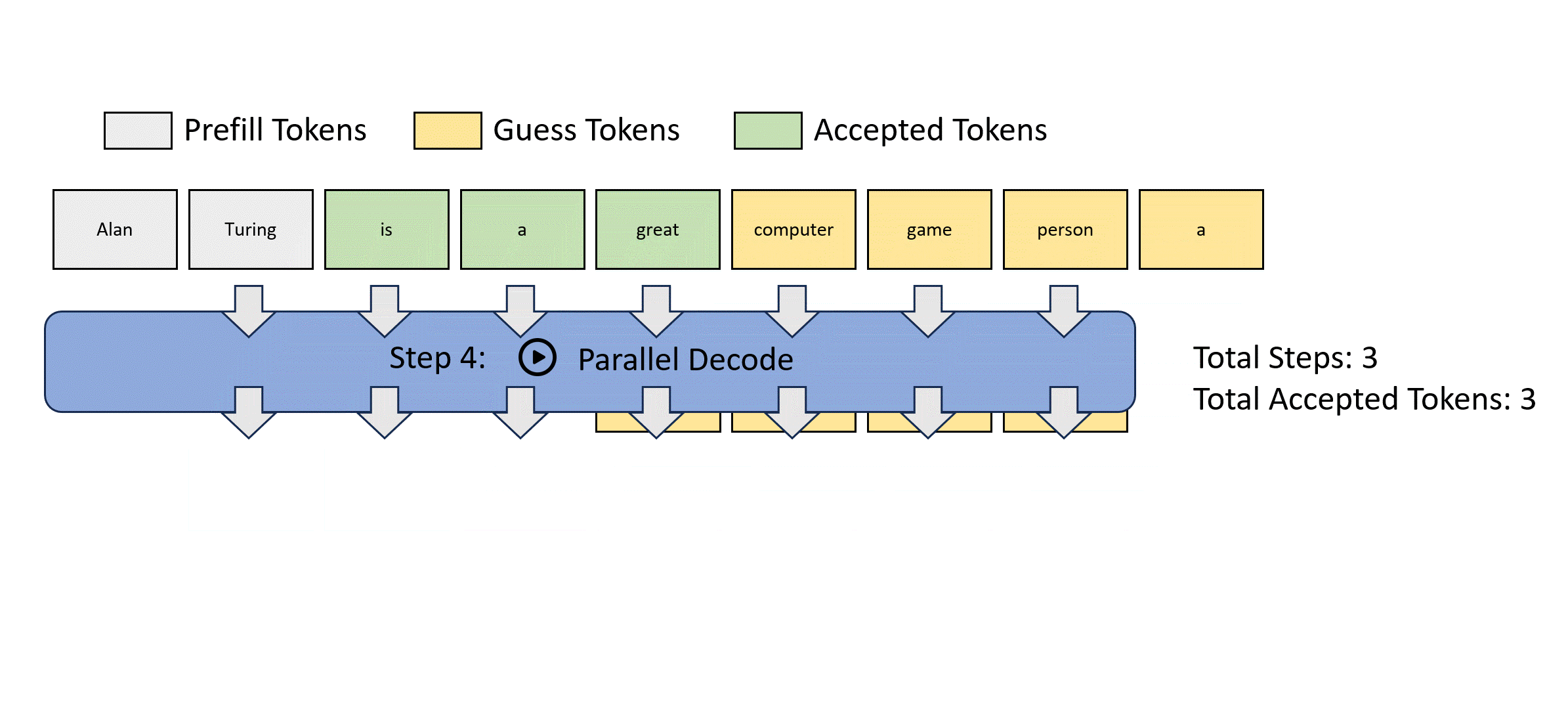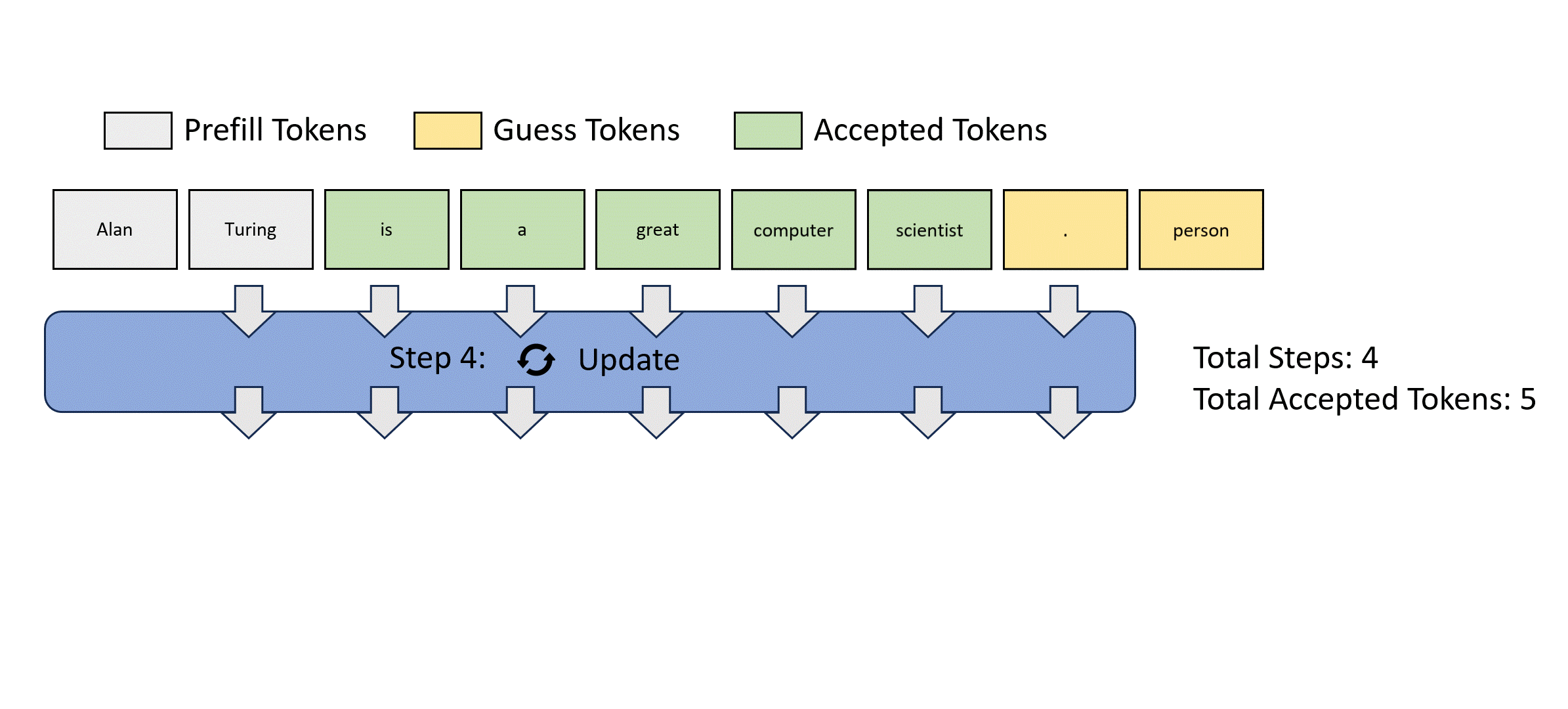
Lookahead Decoding

Lookahead decoding overcomes the limitations of Jacobi Decoding by leveraging its capability of generating parallel n-grams. In Jacobi decoding, we notice that each new token at a position is decoded based on its historical values from previous iterations. This process creates a trajectory of historical tokens at each token position, forming many n-grams. For instance, by looking back over three Jacobi iterations, a 3-gram can be formed at each token position. Lookahead decoding takes advantage of this by collecting and caching these n-grams from their trajectories. While lookahead decoding performs parallel decoding using Jacobi iterations for future tokens, it also concurrently verifies promising n-grams from the cache. Accepting an N-gram allows us to advance N tokens in one step, significantly accelerating the decoding process.

Lookahead Branch

The lookahead branch aims to generate new N-grams. The branch operates with a two-dimensional window defined by two parameters:

• num_speculative_tokens $W$: how far ahead we look in future token positions to conduct parallel decoding.
• ngram_prompt_lookup_max $N$: how many steps we look back into the past Jacobi iteration trajectory to retrieve n-grams.

Here, we look back at 4 steps ($N=4$) in the trajectory and look ahead at 5 tokens ($W=5$) for future positions. In the figure, the blue token labeled 0 is the current input. The tokens in orange, green, and red were generated in previous Jacobi iterations at steps $t-3$, $t-2$, $t-1$ respectively. The number on each token indicates its position relative to the current input token (the blue one marked with 0). At the current step $t$, we conduct one Jacobi iteration to generate new tokens for all 5 positions, using the trajectory formed by the previous 3 steps. Then, we collect 4-grams -- for example, a 4-gram could comprise the orange token at position 1, the green token at position 2, the red token at position 3, and the newly generated token at the current step.

As the decoding progresses, tokens from the earliest step in the trajectory are removed to maintain the defined $N$ and $W$ parameters. It's important to note that when $N=2$, lookahead decoding essentially becomes equivalent to Jacobi decoding.

Verification Branch

Alongside the lookahead branch, the verification branch of each decoding step aims to identify and confirm promising n-grams, ensuring the progression of the decoding process. In the verification branch, we identify n-grams whose first token matches the last input token. This is determined via a simple string match. Once identified, these n-grams are appended to the current input and subjected to verification via an LLM forward pass through them. As the n-gram cache grows, it becomes increasingly common to find multiple n-grams that start with the same token, which raises the verification cost. To manage the cost, we set a cap of $G$ on the number of candidate n-grams considered in the verification branch. In practice, we often set this cap proportional to $W$ (e.g. $G=W$).

Scaling Law for Lookahead Decoding

Lookahead decoding can generate $W$ different N-grams and verify $G$ candidates per step. As $W$ (the number of speculative tokens) and $N$ (the N-gram size) increases, so do the computational operations per step. However, this increase also enhances the likelihood of accepting a longer n-gram with a step. In other words, lookahead decoding allows to trade more flops for reducing latency, provided the system is not constrained by computational capacity.

To examine the scaling behavior of lookahead decoding, we analyze the number of decoding steps required for a given number of tokens, varying the values of $N$ and $W$. The findings are illustrated below. Notably, when the n-gram size is sufficiently large (e.g. $N=11$), exponentially increasing the future token guesses ($W$) can linearly reduce the number of decoding steps. We refer to this phenomenon as the **scaling law **of lookahead decoding.

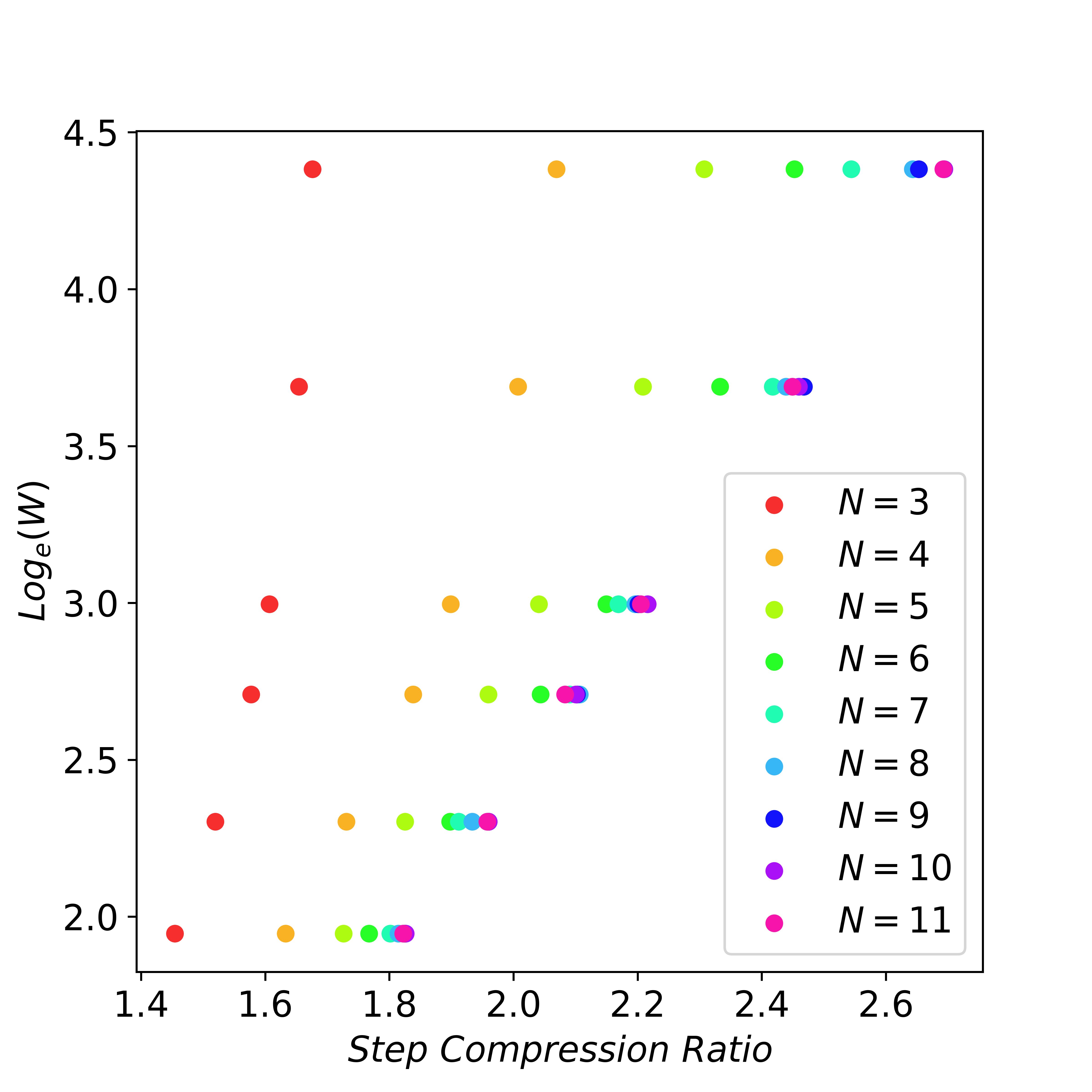
When N is large enough, exponentially increasing window size W can linearly reduce the number of decoding steps. Here we set G = W.